高崎・和算愛好会 掲示板
高崎・和算愛好会 ホームページ
高崎・和算愛好会 管理人ブログ
久しぶり 一関市博物館の解答発表 - 管理人
2024/03/11 (Mon) 16:46:24
令和６年３月１１日 令和５年度「和算に挑戦」の解答が発表されました。
今回は、非常に不安がありましたが、なんとか正解したようです。
例年は、ブログに自分の解答を載せていましたが、今年は、ブログに載せる方法を忘れてしまいました。
Re: 久しぶり 一関市博物館の解答発表 - 小池哲也
2024/03/19 (Tue) 22:56:52
今日、解答集が届きました。今年も何とか正解できてほっとしてます。最近はフーリエ変換の復習をしています。昔、こんなの何の役に立つのかなと､馬鹿にしていたのですが、必要に迫られ復習してみたら、デジタルの信号処理の世界ではすごいことになっていたので驚いています。数学は楽しいですね。
お久しぶりです - 管理人
2024/04/06 (Sat) 16:51:35
書き込み、ありがとうございます。
令和５年度の群馬県からの参加者は、小池さんと２人でした。数年前は、高橋さんという人がいましたが。
今回、岩手県和算研究会会長賞を受賞した、徳島県の清田さんは、群馬県和算研究会のホームページで知り合った方です。
この頃は、以前は出来たことが、出来なくなりました。復習、復習です。楽しいお話を伺いたいと思います。
ブログに書く方法 思い出しました - 管理人
2024/08/20 (Tue) 09:38:46
新型コロナウイルス対応の自粛で陥った フレイル状態から、すこしづつ回復しています
ブログを書く方法を思い出しました
まだ、意欲の減退からは戻りきれていませんが、すこし明るさが見えてきました
回答募集って？ - 匿名希望
2024/05/26 (Sun) 12:31:01
回答するためにはなにか条件があるんでしょうか?
誰でも回答できるわけではないようですね。
Re: 回答募集って？ - 管理人
2024/08/20 (Tue) 09:30:54
すみません 書き込みして戴いているのを放置していました
一関市博物館の「和算に挑戦」は、だれでも参加できます ＷＥＢで問題を見て 解答を郵送するだけです
参加してみるのが良いと思います
問題は３問で、やさしいのから難しいのまであります
２０２４年１２月１日に新しい募集があります
上級問題 - 小池哲也
2023/01/06 (Fri) 22:09:48
今年の上級問題が､やっとのこと解答できました。
とても苦労したので､うれしくてついついメールしてしまいました。
Re: 上級問題 - 管理人
2023/01/07 (Sat) 14:02:36
新年あけましておめでとうございます。
上級問題、もうできたのですか。
早いですね。 わたしはまだ初級問題と中級問題ができたところです。上級は、４乗の式になってしまい、見直し中です。
今年の２月から、群馬県和算研究会のホームページで問題の出題を担当することになりました。よろしければ、解答例の投稿をお願いします。
「和算に挑戦」も、昨年度からまた群馬県からの参加者は、小池さんとわたしのふたりになってしまいました。今年度もよろしくお願いします。
管理人メールアドレス変更しました - 管理人
2022/11/24 (Thu) 15:24:01
２０２２年（令和４年）１１月２５日
管理人メールアドレス変更しました。
忍澄 圓理真術 弧矢弦叩底 - 片野清道
2022/10/04 (Tue) 16:15:57
忍澄のお寺の近くに生まれ育ち、数年前に
はまぐりの数学 美濃・飛騨の国の和算の歴史
https://hamaguri.sakura.ne.jp/minohidawasan.htm
で、忍澄 弧矢弦叩底の事を知り、ネットで検索していて、この掲示板にたどりつきました。さっそく登録しました。
Re: 忍澄 圓理真術 弧矢弦叩底 - 管理人
2022/11/08 (Tue) 16:59:05
投稿ありがとうございます。
半年以上ほったらかしにしており、投稿に気が付きませんでした。申し訳ありません。
はまぐりの数学のホームページも拝見しました。
今年も、１２月１日に一関市博物館から和算問題が出題される予定です。初級問題を小学生たちが自由に考えて答えを出します。その頭の柔らかさは素晴らしいものです。現在数学に侵された大人には、想像ができません。初級問題の解答を応募することをお勧めします。
質問 - うべ
2021/07/12 (Mon) 09:43:39
こんにちは。
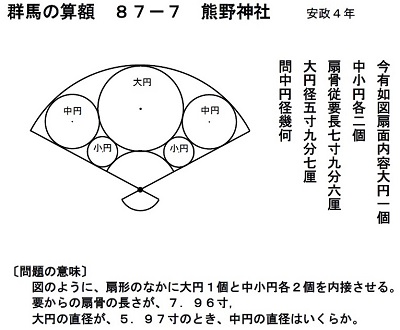
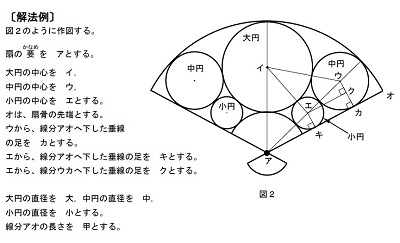
「「和算」やってみませんか！２０１７年に学んだ問題」のページの「群馬の算額８７－７熊野神社」の問題について、わからない点があります。
扇の要（pdfファイル内のア）と、中円の中心（ウ）と、小円の中心（エ）が同一直線上にならぶことの、理由は何でしょうか？
pdfファイルの解法例は、そのことを使って式(1)を導いていると思います。
突然失礼しました。
Re: 質問 - 管理人
2021/08/07 (Sat) 08:47:21
投稿ありがとうございます。
遅くなり申し訳ありません。
小山さん、メールありがとうございます。
小山さんのメールで、８月６日に気が付きました。
問題は、これですね。
Re: 質問 - 管理人
2021/08/07 (Sat) 09:18:32
図２から、 大＝中＋小 としている部分ですね。
これは、一般的に成り立つものではなさそうです。
問題の条件で作図をして見ると、成り立つように見え、確認すると確かに成り立つのですが、簡単な説明ができません。
この解法例は、数学的にダメですね。
別の解法例を考えましょう。
うべさんの解法例を公開可能ならば、
メールに添付して送って下さい。
令和２年の回答 - JR田町 URL
2021/01/21 (Thu) 15:31:17
令和２年の上級の回答は９寸になりました。
正解発表を待ちます。
当方の回答を下記のURLに貼り付けました。
上級問題の回答 - 管理人
2021/03/19 (Fri) 23:19:48
素晴らしい、正解でした。
ＪＲ田町さんの回答をもっと良く見たいとフェイスブックを始めましたが、どうも、ツイッターのようでした。
会長賞おめでとうございます - 小池
2021/03/14 (Sun) 07:58:23
会長賞獲得おめでとうございます。
岩手県和算研究会会長賞を受賞しました - 管理人
2021/03/19 (Fri) 23:10:15
小池さん早いですね。
２月下旬にコメントを求められたので、知っていたのですが、解答集が届くまではフェイクニュースかもと思っていました。１８日に解集と賞状が届き本当とわかりました。
昨年は、できなかったので、群馬県の３人に復活しました。しかし、新しい人が増えませんね。今年はなんとかして増やしたいと思っています。
一関市博物館の「和算に挑戦」載せました - 管理人
2020/12/20 (Sun) 04:44:20
高崎・和算愛好会ホームページに
令和２年度の一関市博物館の「和算に挑戦」
を追加しました。
去年の上級問題は、応募できなかったので、今回は頑張りたいと思います。
「和算に挑戦」解答集が届きました - 管理人
2020/03/09 (Mon) 14:12:43
「和算に挑戦」解答集が届きました。
・ウエノドウさん 上級の部 優秀賞受賞おめでとうございます。
・群馬県からの参加者は３名でした。
増えないですね。
・上級問題の正解者は、４４名です。
昨年の半分です。
・群馬県からの上級問題正解者は、１名です。
小池さんだけです。
・わたしは、中級問題,初級問題は正解でした。
うれしいことに、わたしが会社に勤めていた時の
同僚が、上級問題・中級問題・初級問題の全てに
正解していることです。
素晴らしい！